Aquí está nuestra calculadora de interés compuesto, si lo necesitas más abajo encontrarás las instrucciones para utilizarla.
Instrucciones de la calculadora de interés compuesto
Como puedes comprobar, la calculadora de interés compuesto es totalmente online y está en euros. Ten en cuenta que los cálculos son los mismos independientemente de la divisa.
Estos son los diferentes campos que deberás completar en la calculadora:
- Capital inicial: Es la cantidad de dinero que vas a invertir en un primer momento, que podría ser equivalente a tus ahorros. Si no hay cantidad inicial puedes dejar el campo en 0€.
- Aportaciones anuales: Es la aportación anual de capital que se realiza a la inversión. La calculadora considera que la aportación se realiza al final del año (serían los ahorros recurrentes). Si no hay aportaciones puedes dejar el campo en 0€.
- Duración de la inversión: Es el tiempo en años que durará la inversión. Para poder realizar el cálculo deberás introducir una cifra igual o superior a 1 año.
- Rentabilidad anual: Es la rentabilidad anual esperada expresada en porcentaje. Si quieres utilizar decimales deberás separarlos con una coma.
Si quieres tener más información sobre el interés compuesto, te invitamos a seguir leyendo.
Más información sobre el interés compuesto
Uno de los conceptos económicos clásicos del que todo el mundo ha oído hablar centenares de veces pero que la mayoría no termina de entender es el interés compuesto.
¿En qué se diferencia del interés simple? ¿Cuáles son las operaciones más habituales en las que se utiliza? ¿Cuánto podemos esperar que crezca una inversión gracias al mismo?
En este artículo no solo vamos a responder a las preguntas más habituales. También podrás comprobar los cálculos con nuestra calculadora de interés compuesto online.
Veamos si Einstein estaba en lo cierto…

¿Qué es el interés compuesto?
Un experimento muy conocido en psicología demostró que la capacidad de posponer una gratificación era un factor clave para alcanzar el éxito.
Hablamos del marshmallow test o prueba del malvavisco.
El experimento consistía en ofrecer a varios niños una golosina (la comúnmente conocida «nube») y decirles que podían comérsela justo en ese momento o esperar unos minutos y, a cambio, recibir dos golosinas como premio a su espera.
Se observó que los niños que eran capaces de resistir la tentación y esperar para recibir un premio mayor tenían, ya como adultos, más éxito tanto profesional como personal.
Esa capacidad de posponer la recompensa es la esencia de la inversión con interés compuesto.
Te vamos a explicar por qué.
El interés compuesto es el interés originado por un préstamo o inversión que tiene una característica única: en lugar de cobrarse, se capitaliza. Eso significa que en cada periodo, al capital inicial se le suman los intereses generados en el periodo anterior, generando a su vez más intereses en el siguiente periodo.
Con un ejemplo todo es más sencillo.
Mira.
Si hoy inviertes 1.000€ y recibes un 10% anual, los 100€ que recibirías el primer año se incorporan al capital, por lo que el segundo año la inversión generaría un 10% de 1.100€, es decir, 110€. Si esto lo repetimos año tras año el capital empieza a aumentar de forma exponencial.
¿Y cuánto es razonable esperar de una inversión?
Fíjate en estos dos gráficos en los que se explica cómo habrían rentado diferentes tipos de inversiones desde 1900 si se hubiera reinvertido el interés. No te dejará indiferente.
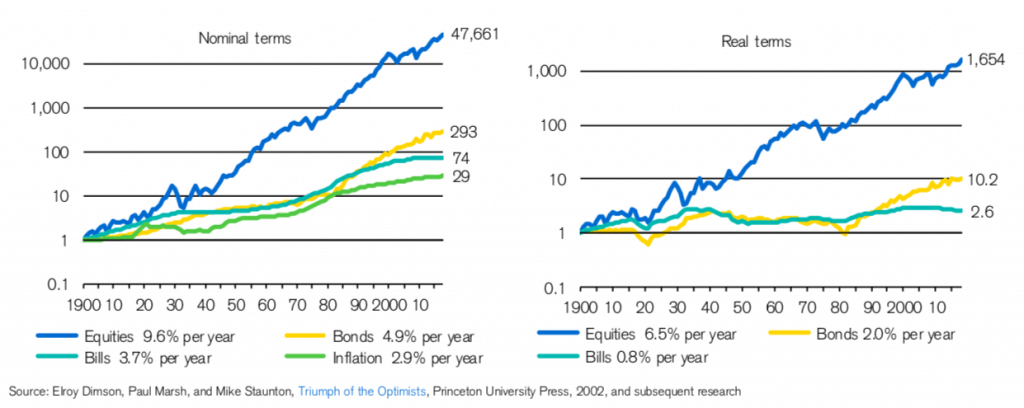
El de la izquierda representa el valor en el tiempo de una inversión de 1$ en diferentes activos desde el año 1900 hasta 2018 en Estados Unidos.
La línea de más rentabilidad son acciones, la siguiente Bonos del estado, la azul clara Letras del tesoro y la línea verde, la más baja, marca la inflación, que convierte 1 dólar de 1900 en 29 dólares de 2018.
La gráfica derecha marca la misma evolución del valor de los activos pero en valor real, es decir, excluyendo el impacto de la inflación. En estos 118 años, una inversión de 1$ en acciones que reinvirtieran los intereses habría crecido 1.654 veces en poder adquisitivo. Casi nada.
Atendiendo al tipo de activos, de nuevo, tras las acciones se sitúan los Bonos del Estado, que con una rentabilidad anual del 2% solo habrían aumentado 10,2 veces. En el caso de las Letras del Tesoro (Treasury Bills) en 118 años apenas se multiplica por 2,6.
Entonces, ¿merece la pena el interés compuesto para un 0,8% anual? Algo es mejor que nada pero, como vemos, no cubre la inflación ni de lejos. Estarías perdiendo poder adquisitivo año a año.
¿Quieres hacer crecer tus ahorros con interés compuesto?
Nosotros somos partidarios de invertir a largo plazo en productos con bajas comisiones como pueden ser los gestores automatizados o los fondos indexados de bajo coste.
Eso sí, ten en cuenta que rentabilidades pasadas no aseguran rentabilidades futuras y que el interés compuesto no es magia; en la práctica, las rentabilidades nunca son iguales aunque la fórmula así lo asuma.
Diferencia entre el interés compuesto y simple
En el interés compuesto los nuevos rendimientos generados pasan a engrosar el capital en cada periodo, mientras que en el interés simple no sucede así; los intereses siempre se calculan sobre el capital inicial. Por lo tanto, el interés simple no permite un crecimiento geométrico.
Si inviertes 1.000€ a plazo fijo en cualquier entidad financiera recibirás la liquidación de intereses mensual, anual o del periodo que corresponda. En un interés compuesto, estos se capitalizarán y se tendrán en cuenta para el siguiente cálculo de intereses. Mientras que con el interés simple recibirás siempre la misma cantidad de intereses.
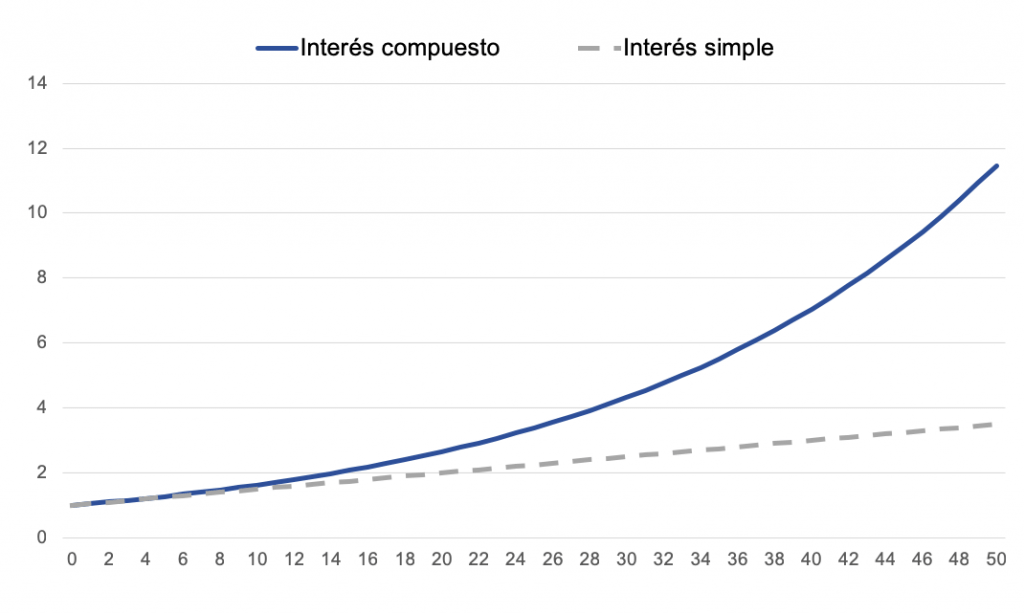
Fórmulas del interés compuesto y simple
El cálculo del interés simple lo podría hacer un niño (con una calculadora). La fórmula es la siguiente:
Capital final = Capital inicial (1 + n * i)
Siendo i la tasa de interés y n el periodo de tiempo
Si inviertes 1.000€ durante 10 años a un 5% anual, al vencimiento tendrías:
Capital final = 1.000 (1+10*0,05)
Capital final = 1.500,00€
El rendimiento total de la inversión sería de 500€ en 10 años.
Para calcular el interés compuesto usaremos otra fórmula financiera un poco más compleja pero que tampoco requiere ser un experto en matemáticas:
Capital final = Capital inicial (1+i)^n
Si hacemos la misma inversión de 1.000€ a un 5% anual:
Capital final = 1.000 (1+0,05)^10
Capital final= 1.628,89€
El rendimiento total de la inversión sería de 628,89€ en 10 años.
Como ves, esperar esos diez años sin recoger intereses, reinvirtiéndolos, aporta 128,89 euros más. Si la liquidación de intereses fuese mensual en lugar de anual la cantidad resultante sería ligeramente mayor, ya que estaríamos poniendo antes a trabajar parte de los intereses.
El interés compuesto con aportaciones
Imagínate ahora que además de las aportaciones provenientes de las liquidaciones de intereses hacemos aportaciones constantes al capital (como es posible hacer con nuestra calculadora en euros). Esas nuevas aportaciones generarán más intereses que se volverán a capitalizar.
La idea es crear una bola de nieve que engorda poco a poco. Si le damos un empujón a la propia retroalimentación que supone la capitalización de los intereses el resultado será un crecimiento cada vez mayor de esa bola de nieve.
A este modelo de interés compuesto con aportaciones se le conoce como “basic investment” y tenemos que hacerle unos arreglos a la fórmula del interés compuesto para calcular su rendimiento:
Capital final = Capital inicial (1 + i)^n + c[ ((1 + r)^(n + 1) – (1 + r)) / r ]
Siendo c las aportaciones de capital
Si tenemos un aportación anual de 100€ al año, durante 10 años:
Capital final = 1.000 (1 + 0,05)^10 + 100 [((1+0,05)^11 – (1+0,05)) / 0,05]
Capital final = 1.628,89 + 100 [0,66/0,05]
Capital final = 1.628,89 + 1.320,67
Capital final= 2.949,56€
Parece que hay que ser Einstein para calcularla, pero no es para tanto. Bueno, tal vez sí, pero para eso tenemos las hojas de cálculo.
Cómo calcular el interés compuesto en Excel
Si quieres hacer el cálculo de forma automática puedes usar una hoja de cálculo. Para ello tenemos una fórmula llamada Valor Futuro (VF).
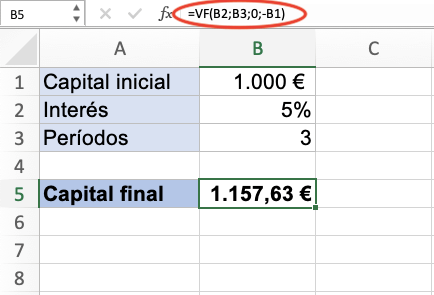
Los argumentos que necesita son los mismos elementos que encontramos en la fórmula original:
- Tasa de interés
- Número de periodos
- Aportaciones
- Capital inicial
- Tipo (indica en qué momento se hacen las aportaciones y si computan para un periodo u otro)
Te invitamos a que hagas números por tu cuenta. Es bastante sencillo.
Albert Einstein y el interés compuesto
A poco que hagas unas búsquedas en Google sobre el interés compuesto te encontrarás con una leyenda sobre una frase atribuida a Albert Einstein.

La frase la encontrarás expresada de diferentes maneras, aunque el mensaje suele ser el mismo:
«El interés compuesto es la fuerza más potente del universo.»
No es necesario ser un experto en la trayectoria del genio de la relatividad para percatarse de que, si es cierto que lo dijo, fue con algo de guasa.
La dudosa veracidad de la atribución viene, principalmente, por la fecha. Einstein falleció en 1955 y no hay noticias de la famosa frase hasta los años 80. Tampoco hay pruebas visuales o por escrito de que en algún momento la pronunciara…
En cualquier caso, la importancia del interés compuesto en la vida diaria es indudable. Las entidades financieras saben de su potencial y lo utilizan en los préstamos hipotecarios. En este caso, la capitalización juega en contra tuyo y a favor del banco.
Ya tienes otro argumento para no endeudarte.
En resumen, tanto si vas a ser inversor como el receptor de un préstamo, conocer cómo funciona el interés compuesto es imprescindible.
Si quieres hacer tus propios cálculos puedes utilizar nuestra calculadora online de interés compuesto.
Fuentes:
Credit Suisse Global Returns
Einstein fact-check
Wikipedia


Donde y como se contratan este tipo de productos
Hay algún tipo de riesgo en estas inversiones?
Me gustaria realizar una inversion. Tienes contacto para asesoramiento?
Saludos y gracias por el articulo
Buenos días Pamela, puedes enviar un mensaje desde la página de contacto:
Formulario de contacto
Hola…muy interesante…mi pregunta es como se calculan los fondos de pension ya que en ellos uno aporta mensualmente….se capitaliza mensualmente? Es decir aportaciones y lo correspondiente por intereses por periodos mensuales?? O si importar cuanto uno aporte mensual igual hasta cerrear un año se capilaizan ambos??
Hola Carlos, dependerá de cada producto financiero así como de la evolución de los mercados.
Un saludo.
Buen articulo!
Como cambiaria la formula de interés compuesto con aportaciones anuales, si la aportación anual aumenta un 5% respecto la aportación del año anterior.. es decir una «c» que aumente cada año un 5%.
Hola Ernest, gracias por la sugerencia, la tendremos en cuenta si actualizamos el cálculo 🙂
Claro, todo muy bien explicado, pero como consigo que mi inversión inicial rente todos y cada uno de los años un 10%, es muy complicado, por no decir imposible, con que productos.
Gracias por el artículo.
Mira en youtube el canal de Visionarios bolsa, y veras que un 10 porciento al año no es dificil.
Nosotros somos más partidarios de asumir un 5%, creemos que es más razonable a largo plazo.
hola buenas tardes, que fondos indexados en España aplicaría el interés compuesto?
los de acumulación?
muchas gracias un saludo
Hola Jose, así es. Se reinvierten los dividendos y se revaloriza su valor por lo que a largo plazo de aplicaría el interés compuesto.
Un saludo!
Hola que tal!
La respuesta es sencilla, un fondo indexado al SP500, la media de revalorización histórica ronda el 10% , la comisión es de un 0,10%…
Una aportación fija cada mes y casi que te puedes olvidar….
Puedo yo aportar más o menos al monto fijado un ejemplo si mi capital inicial son 10000$
Y mi aporte al capital al año es de 5000$ pero quiero en x año aportar 7000$ puedo hacerlo?
Claro, tú puedes invertir lo que te dé la gana, cuando te dé la gana, en lo que te dé la gana.
Como si quieres invertir X euros al mes todos los meses, y luego un mes no invertir nada, y otro invertir el triple.
La verdad es que había oído hablar del interés compuesto pero nunca había hecho una simulación y es BRUTAL.
Gracias Guillermo vuestra ayuda promoviendo la cultura economica
Cómo se q en un fondo de inversión se está aplicando el interés compuesto?
Muchas gracias
En principio todos lo hacen si obtienen una rentabilidad positiva, especialmente los que acumulan los dividendos.
Un saludo Mayte!
Muy interesante
Muchas gracias Rafael! 🙂